ELSI researchers use a representation of chemistry by rules, which operate one level lower than molecules and reactions, to understand how simple mechanisms generate complex networks. They then study how the small number of rules and their relations tame the complexity of the large networks they generate in ways that are not apparent from the reaction networks alone. Problems of biochemical function sometimes turn out to have repetitive and even program-like structures in such spaces. One can identify naturally occurring solutions like universal metabolic pathways as optima that minimise programme complexity or energy cost in chemical spaces that are comprehensible to us and to selection because of regularities imposed by the rules.
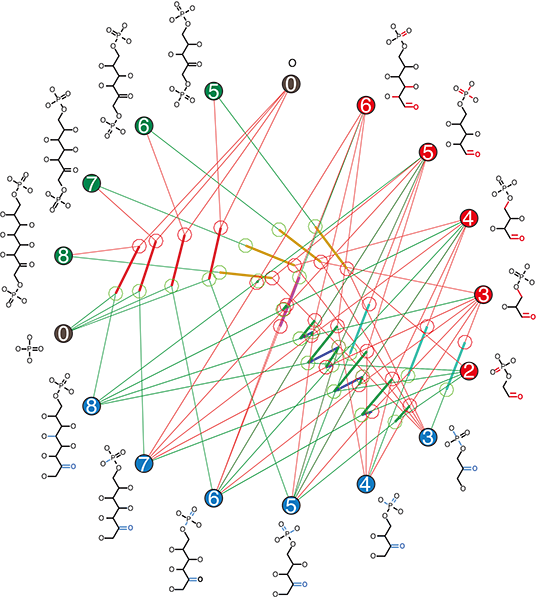
A common reason many natural processes are complex is that objects can’t undergo changes individually: one object can change only if other objects also change as part of the same event. For example, Carbon dioxide can only turn to methane if other molecules donate hydrogen and remove oxygen. An egg cell can only become an embryo when it fuses with a sperm. You can only play a game of Bridge when you have four players. The need to have multiple parts “lined up” to change together can cause remote parts of a system to constrain each other, making the system hard to understand, predict, or control. (Who hasn’t heard Bridge players unable to start their game, saying, “We can’t find a fourth!”) Chemists have a word, stoichiometry, for this kind of change in which a whole set of objects is converted together at once, and chemical reaction networks are also known as stoichiometric networks.
Stoichiometric networks are often large and complicated, with many species and reactions, and it can be hard to understand how they couple cause and effect. Yet we know many cases in which evolution has sifted through this complexity to find specific solutions and maintain them for a long time. Examples include the universal pathways of metabolism, such as the Calvin-Benson-Bassham cycle for fixing CO2 to biological sugars (the name given to the process by which inorganic carbon enters living systems). Do the chemical networks we find on planetary surfaces and in cells have hidden simplicity that makes searching and controlling them possible for the kinds of random processes needed to account for life’s origin? The answer is yes: many networks in nature have reactions generated by just a few rules. In chemistry, these are known as the reaction mechanisms. The difference between a reaction and a rule is that reactions convert specific molecules: rules describe the chemical bonds that change, no matter what molecules they occur in, for example, changing a bonded –H to a bonded –OH. If one can control the rules, one may be able to understand and evolve the networks they produce.
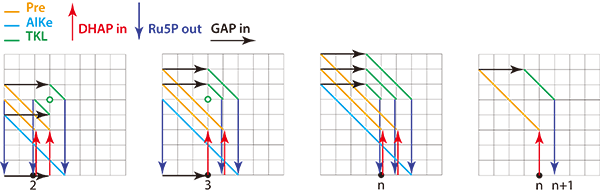
A project by ELSI’s Specially Appointed Professor Eric Smith and Specially Appointed Associate Professor Harrison Smith, and their collaborator Jakob Andersen, Associate Professor at the University of Southern Denmark (himself a former ELSI EON fellow), aimed to understand how rules simplify reaction networks, and how we can use this simplicity to identify the reasons evolution has produced a universal Calvin cycle and maintained it for more than 3.5 billion years. They used a dedicated computer language for rule-based computational chemistry, called MØD, written by Andersen and colleagues, to model the messy networks generated by only five rules in the absence of selection for individual chemical species (Fig.1). They then studied the common features among all reaction sequences that do what the Calvin cycle does: shuffle CH2O groups between sugars of different lengths without loss. They were able to show that solutions to this problem can have an algorithmic structure, with an initialisation reaction and a repeated chemical WHILE loop, followed by a RESET reaction (Fig.2). Among all solutions of this kind, the biological Calvin cycle is the shortest one from feasible chemicals. Also, it requires one of the lowest consumptions of chemical work to perform under typical biological conditions.
The researchers are currently using MØD and similar methods to study more complex and older reaction networks, such as those in prebiotic geochemistry and the earliest metabolisms. Andersen and others have also used the same methods to solve problems in metabolic engineering and optimisation.
| Journal | PLoS Complex Systems |
| Title of the paper | Rules, hypergraphs, and probabilities: The three-level analysis of chemical reaction systems and other stochastic stoichiometric population processes |
| Authors | Eric Smith1,2,3*, Harrison B. Smith1,4, Jakob Lykke Andersen5 |
| Affiliations |
|
| DOI | 10.1371/journal.pcsy.0000022 |
| Online published date | 5 December 2024 |
